Tech Article


Published on:
Inertial navigation using quantum sensor technology is a new field of research and development that can completely revolutionize navigation systems. This novel technology increases inertial measurement accuracy by orders of magnitude over current benchmarks. This can enable absolutely reliable inertial navigation systems (INS) that can operate entirely standalone and retain accuracy over the course of years rather than months using current technology.
At the moment, the GNSS (satellite-based navigation) serves terrestrial requirements for determining position and heading, however, the increasing reliance on GNSS for technologies, infrastructure, products and services also makes it a vulnerability. By that, meaning that should it be compromised due to jamming and spoofing, which is far more common that one might think, experience equipment failure or be affected by cosmic phenomena such as solar emissions for example, the ongoing effects, disruption and costs will be enormous.
Any time that a vehicle or system that relies on GNSS for navigation, where GNSS is not available, will typically use an INS to perform dead-reckoning. This will plot the vehicle course based on estimates of velocity, heading and direction. The INS will use “classical” (non-quantum-based) sensors to determine acceleration. An INS that uses classical sensors can be regarded as temporary means of navigation due to bias and drift errors that are inherent in classical sensors – these errors affect accuracy of estimated/calculated position and usually build over time and with each change in acceleration detected. To put this into context and depending on vehicle type and application, the highest grade classical INS may be able to retain accuracy for several months; while a low-grade INS may be relied upon for perhaps seconds only. The position error of an INS continues to accumulate over time and distance, until an absolute position reference can be made via GNSS or some other source. At this point, the INS is able to clear accumulated error and reset position based on the updated absolute position data. Without this reset/recalibration, any “classical” INS will eventually lose position accuracy.
Undersea, underground and outer space navigation applications already cannot use GNSS as a reference due to non-availability. In such scenarios, higher accuracy dead-reckoning would be an immediate benefit. To make prolonged and accurate dead-reckoning possible without GNSS, quantum sensors may be a solution.
The idea of applying quantum sensor technology into a dynamic environment for the purposes of navigation is a new area of research that presents several specific challenges. Typically, existing research for quantum sensing is based around stationary gravity measurement. This can be used for many applications such as identifying subterranean water and its movement, mineral deposits, monitoring ocean currents and detecting volcanic activity.
In the 1920s, French physicist Louis de Broglie hypothesized that a particle (combination of protons, electrons, neutrons) possesses both particle and waveform properties. This wave-particle duality is integral to the theory of quantum mechanics. This duality applies to atoms also, which are specific combinations of particles that make up physical elements. Due to the lack of physical size of atoms and their electrically charged nature, they are sensitive to almost any change in environment. In response to a change in environment, the atom waveform will alter. It is this tiny waveform that, if changes in it can be measured, can provide accuracy that has prior been the stuff of science-fiction.
Quantum theory has been furthered by many physicists, such as Erwin Schrödinger, in developing hypotheses that help further define quantum mechanics and the mathematics that can help explain its functions. The basics of quantum systems are to exploit the extreme sensitivity of atoms to their environment. Not only that, but because atoms are the basic building block of elements, they are impervious to fatigue, wear or time and have identical inertial characteristics if they are on Earth or somewhere in space. The “purity” of using atoms as a basis for measurement is that there is virtually zero drift. An example being to use atomic clocks to maintain accurate synchronization in critical systems, such as GNSS. Critically, the waveform of an atom remains stable until an external force is applied to it. For example, any change in acceleration, rotation, gravity or electromagnetic field are “felt” by atoms, which subtly affects the atom waveform. The change in waveform can be detected and extrapolated to an actual value through interferometry.
Interferometry is basically the process of splitting a waveform, sending it on two different paths then recombining them and measuring any difference between the original and combined waveforms. A simple example of waveform interference can be observed when ocean waves coming from different directions “interfere” with one another. This may result in a larger wave if the peaks of the waves combine, or a diminished wave if the peaks of one wave meet the troughs of the other.
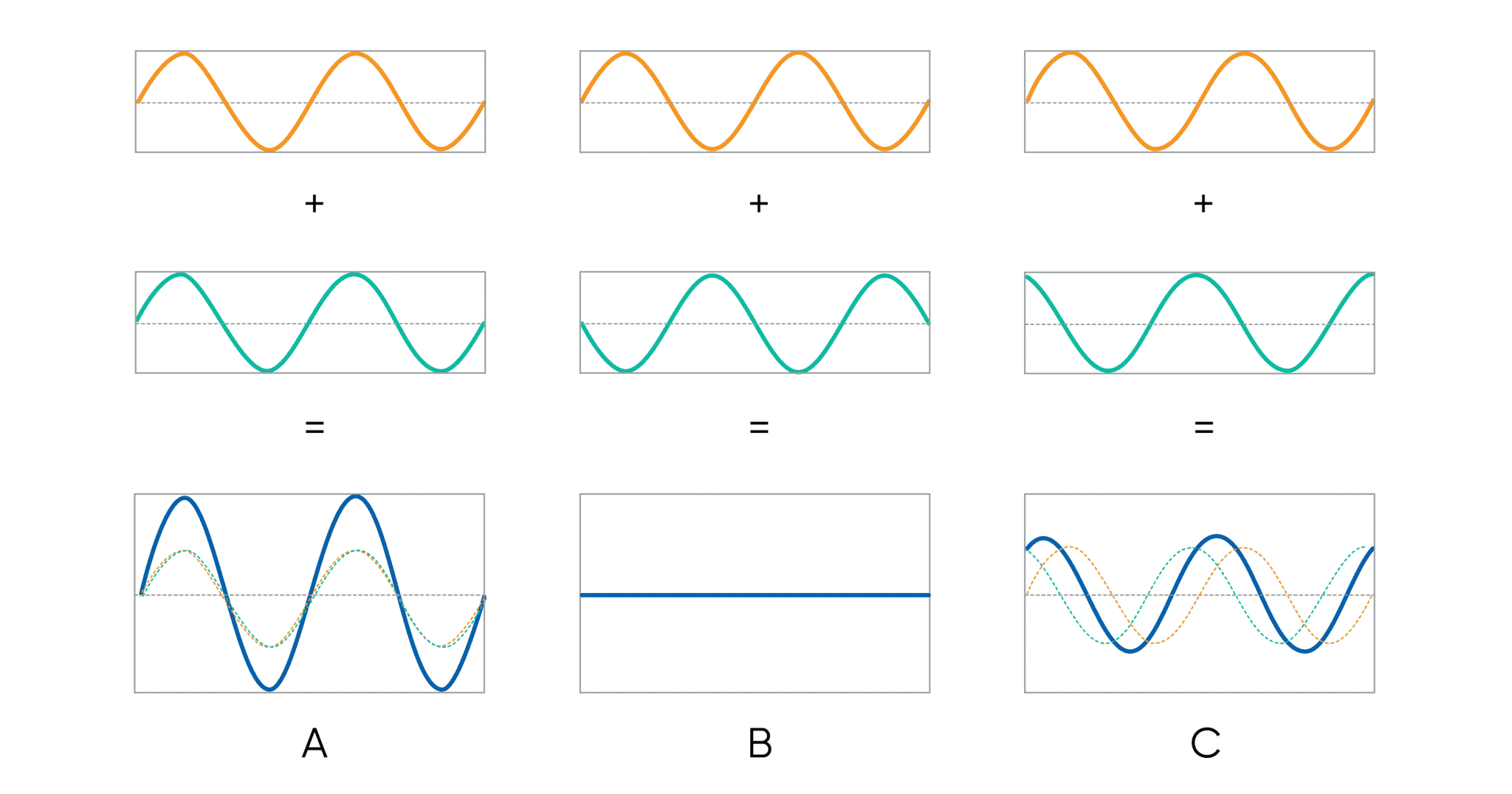
In the example image, the waveforms in (A) (orange and green) are in phase. When combined, the resulting waveform (blue) is larger – this is constructive interference. In (B) the waveforms are out of phase by 180° (inverse to one another). When combined, the resulting waveform is flat (zero amplitude) – this is destructive interference. In (C) the waveforms are out of phase by a small amount. When combined, the resulting waveform has a slightly larger amplitude than the original waveforms – this is constructive interference
As an example of interferometry using light as the waveform, the light is directed toward a mirror that is semi-coated in reflective material. This semi-reflective mirror allows half the light to pass through and half to be reflected, splitting the light. Secondary mirrors will redirect the light so that it recombines.
If the position or angle of one of the mirrors changes due to some external force, say, gravity by even a tiny amount, the waveform of the deflected light will shift in relation to the reference light waveform (phase shift). When the light waveforms are recombined, there will be measurable differences in the waveform fringes (the edges) where parts that were dark now have light and vice-versa. This is an extremely accurate means of measurement due to the very short wavelength of light.
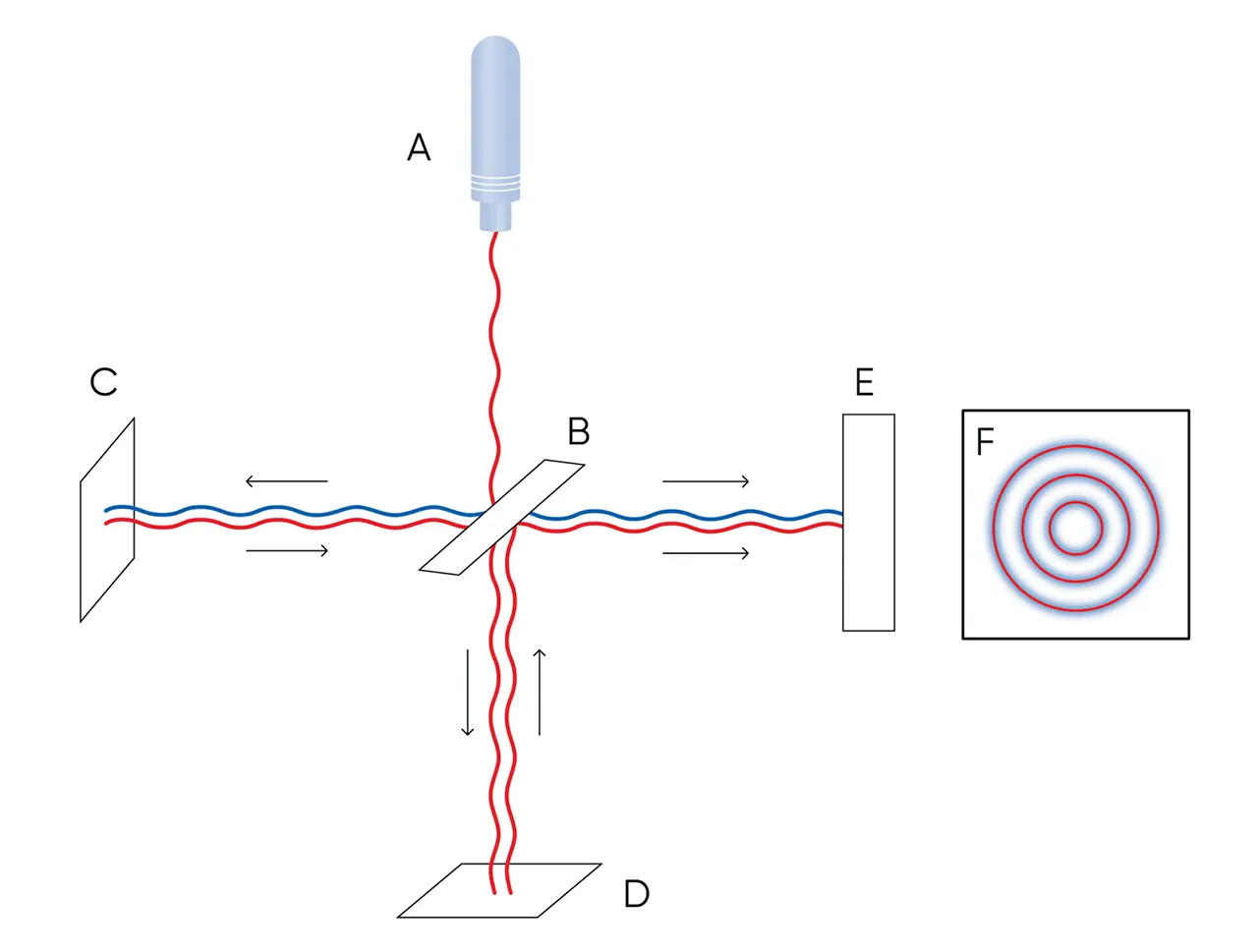
In a basic laser interferometer, laser light (A) is directed towards a semi-reflective mirror (B) – the light splits towards mirrors (C) and (D) and light detector (E). Light reflected from mirrors (C) and (D) is reflected by (B) to (E). The waveform fringes can then be overlaid (F) to calculate the extent of any difference between waveforms
The wavelength of atoms, depending on the substance, is approximately 3 x 104 times smaller than that of visible light. Using the concept of waveform interferometry using atoms represents a level of accuracy that can be mind-boggling.
Similar to splitting the waveform of light using mirrors, the waveform of atoms can also, in a sense, be “split” at the quantum level. This is because the laws of quantum physics allow an atom to exist in all of its possible states at the same time. The ability of an atom to be in multiple states at the same time, as bizarre as this sounds, creates a waveform differential that can be used for interferometry.
Millions of atoms, referred to as an “atom cloud”, are typically required for an interferometer experiment. The greater the number of atoms, the greater the potential accuracy of measurement. Prior to the atom cloud being split, it is cooled using lasers. Laser cooling may sound paradoxical, however, it works because photons from the laser are absorbed and re-emitted by the atoms, which causes them to lose small amounts of kinetic energy at each emission. After thousands of photon absorption and emissions, the atoms become cooled to just above “absolute zero” (0° kelvin or -273.15° C). This super-cold temperature causes the atoms to have virtually no energy and are almost still rather than moving at hundreds of meters per second. In this state, the atoms can be observed and measurements can be taken.
After the atoms are cooled, the cooling lasers are deactivated and the atoms go into free fall. During free fall, the atoms pass three laser pulses. The photons from the first pulse transfers momentum to the cloud and places the atoms into a quantum “superposition” of two simultaneous, spatially separated momentum states. That is, the atoms have a state of being excited by the photons and also not being excited, where the excited state has different momentum to the non-excited state. This effectively splits each atom waveform into two, shifting one in relation to the other to provide the separate paths required for interferometry. After a period, a second laser pulse is directed at the atom clouds to invert the momentum difference between them and cause the atom waveform states to begin converging, effectively to recombine and interfere the waveforms. After a period, a third pulse is used to end the interferometry sequence. The atoms are subjected to a final light pulse which probes their internal state and provides a measurement. Any effect that modifies the potential, internal, or kinetic energy of the atoms via inertia, gravity, electro-magnetism, radiation etc becomes visible in the waveform as a phase difference since they become intrinsic to the quantum mechanical state of the atom. The interference signal manifests as what is referred to as a population difference between final momentum states.
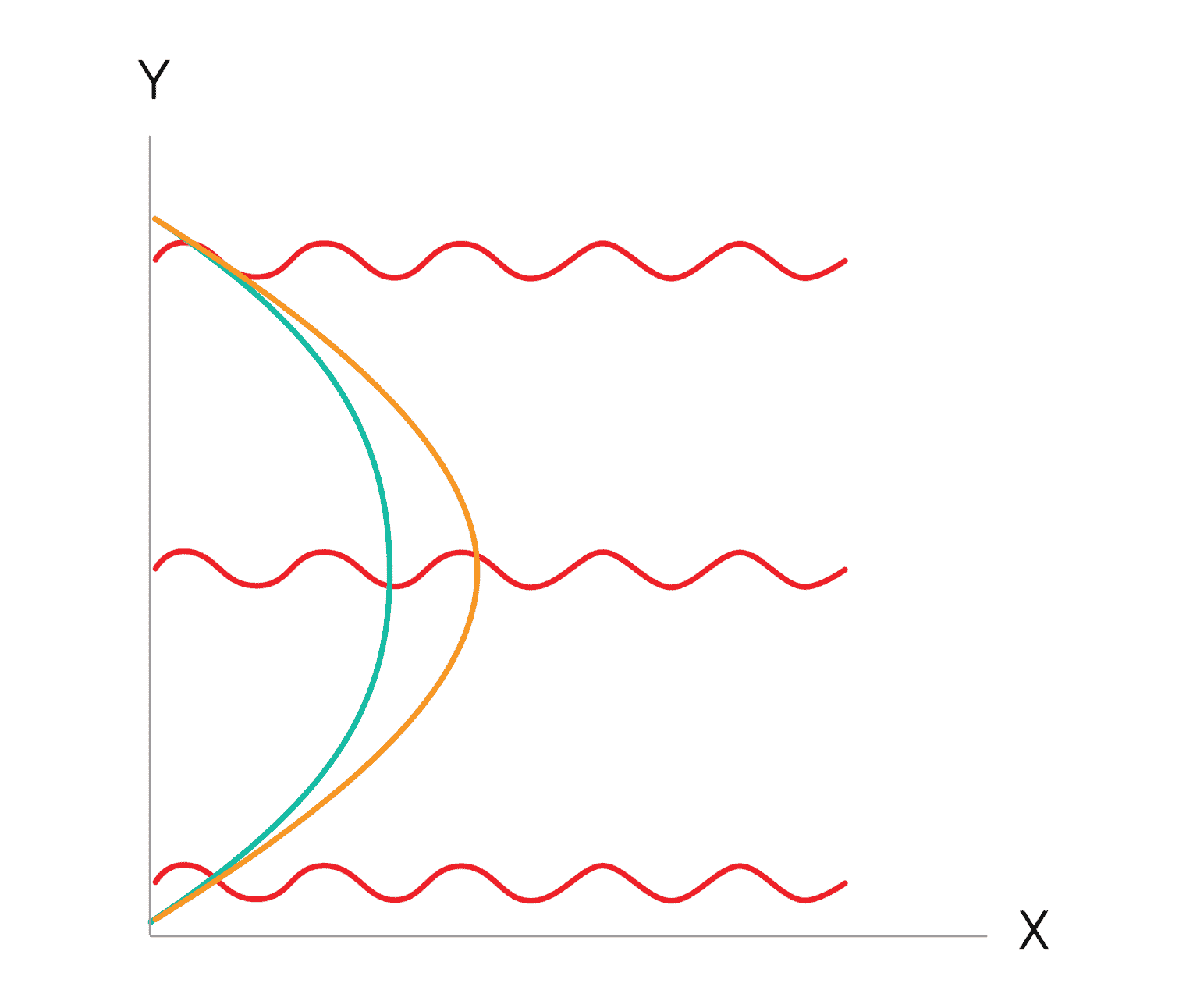
In the example image, the X-axis represents spatial distance and the Y-axis represents time. The red waves represent the laser pulses. The first (lower) pulse imparts photon energy to the atoms and causes a change in momentum. The momentum duality of the atoms is represented by the green and orange lines. The second (middle) pulse inverts the momentum, causing the atoms to merge. The third (upper) pulse ends the sequence, after which the waveform comparison and measurement is made
As an analogy for an atom interferometer, think of the atoms as baseballs and the laser as a baseball bat. The cooled atoms are dropped into the interferometer and the bat hits them upward, which imparts photon energy to the atoms. Due to quantum superposition, the atoms are simultaneously hit and missed by the bat and so are both falling (missed) and going up/stationary (hit). The hit and missed atom states provide the two “arms” or “paths” of the interferometer. The next laser bats the atoms, but in the opposite direction and the third laser stabilizes the atoms.
A fundamental challenge to quantum sensor technology is harnessing the range and bandwidth of acceleration that quantum systems can detect. This is because of their enormous sensitivity.
Let’s define range, bandwidth, and accuracy first.
To put this into the context of comparing classical and quantum sensors, the following data shows differences between properties:
| Classical | Quantum | |
| Bandwidth | 300 to 500 Hz | 0.5 to 2 Hz |
| Range | ±15 g | ±1.2 g |
| Accuracy | 500 µg (micro-g | 10-8) | 10 pg (pico-g | 10-12) |
As can be seen, classical sensors are capable of providing data hundreds of times more frequently than quantum sensors, which, depending on how quickly a change in motion occurs, allows them to capture the entirety of the motion. As a result of this, there is less likelihood of errors caused from having a low bandwidth and “missing” changes in acceleration due to them occurring between measurements.
Of course, with quantum bandwidth being so low, it will be prone to missing rapid changes in acceleration. As a result, acceleration beyond the range of quantum sensors will likely be ambiguous and such data must be considered erroneous.
A method to work around the range and bandwidth limitations of quantum sensors is to fuse the output from them with classical inertial sensors (MEMS, FOG or RLG). Classical inertial sensors can provide the bandwidth and range, while the quantum sensors provide extreme accuracy without error or noise. For quantum sensors, the bandwidth that sensing takes place is typically 1 Hz (once per second). Note that cold atom interferometry sensitivity increases with the greater the duration that the atoms are inside the interferometer (the greater the duration, the lower the bandwidth). For fast moving vehicles, a low bandwidth represents many gaps in the tracking of acceleration as well as potentially generating unusable data by being outside the quantum range.
The output from the cold atom interferometer provides a waveform, where each point on the curve corresponds to unique acceleration. A problem with this is that the waveform is constant and that the peaks of the waveform may vary without being able to determine what the actual measurement is. For example, one peak may represent 1 m/s2 and another identical peak may represent 2 m/s2.
This is where the classical sensor is used due to its high update rate and high dynamic range. Advanced Navigation has developed techniques to:
Fusing the quantum and classical sensor data accurately and reliably requires a highly sophisticated artificial intelligence neural network based system. This applies algorithms to converge data from both sensor systems to remove noise and errors and to combine the data in a meaningful way.
Having high bandwidth sensors allows the detection of changes more frequently than the bandwidth of the quantum sensor. And, even though the classical sensor has error, by fusing the two in an algorithmic way, we can attain the extremely low error of the quantum sensor. Furthermore, a system that is capable of learning will use previous data to continually refine current measurements and cause the system to improve accuracy and precision over time, rather than for it to degrade.
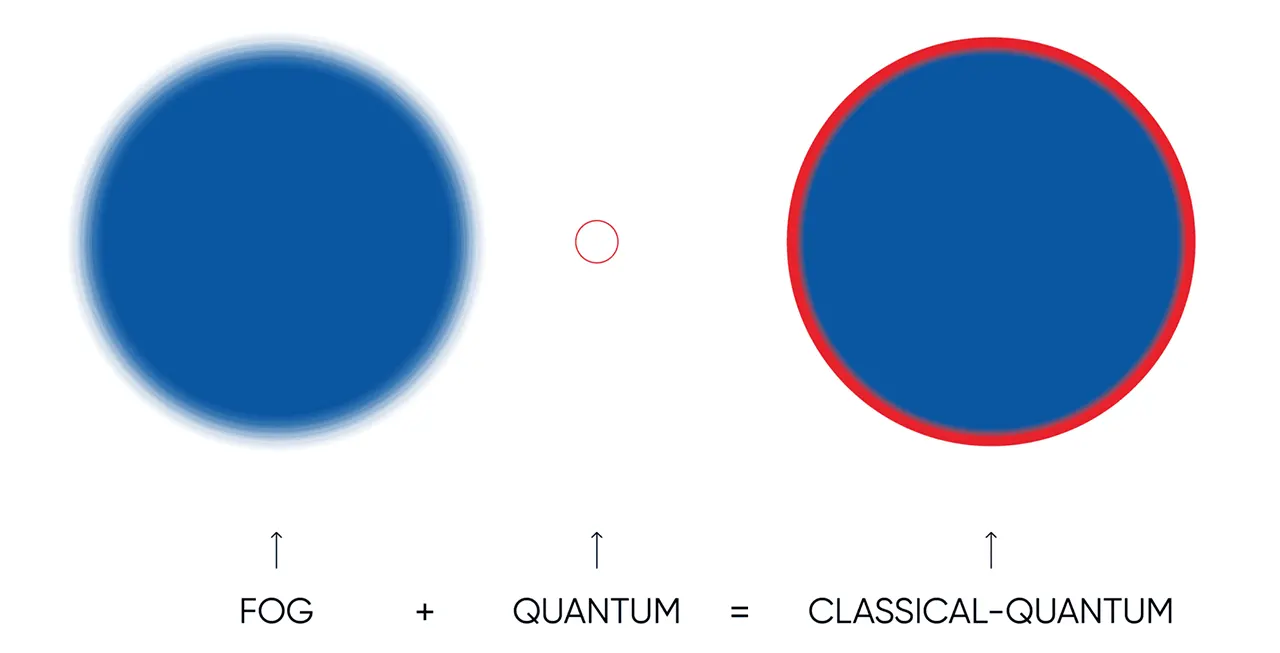
Fusing the bandwidth and range of FOG classical sensors with the accuracy of quantum sensor hardware massively extends the capability of both sensors by effectively removing drift from the classical sensor and increasing range of the quantum sensor
Isolating atoms from the environment for sensing purposes and deploying it to a dynamic vehicle has been a major challenge to quantum sensing. Without a super-controlled environment to trap, launch and control the atoms during interferometry, it would be impossible to gain anything meaningful or coherent in terms of measurement. Also, using bespoke and extremely specialized and expensive lab equipment for the necessary isolated environment for quantum interferometry is not a viable solution for use in real-world scenarios. In response to the hardware challenge of quantum solutions, Advanced Navigation has developed its own hardware suitable for quantum sensor technologies. This hardware is in a form factor that is practical in real-world terms and negates magnetic field interference, and isolates against vibration, shock and rotation using passive (mechanical) and active (computer controlled) systems.
Currently, the highest performing classical inertial navigation systems may be able to provide an acceptable level of dead-reckoning for several weeks before drift and error accumulation become unacceptable. Applying the exceptional stability of quantum sensors as a means of providing accurate measurement outside the normal limits of the classical sensor means drift is negligible and recalibration is rarely required. As a result, dead-reckoning can be extended possibly to years before errors accumulate to the point of being a problem. This will be especially valuable in long distance and extended duration autonomous space missions.
“The Advanced Navigation classical-quantum solution eliminates limitations in sensor range and bandwidth, and massively improves accuracy. As a technology to base the future of inertial navigation on, classical-quantum sensing has given us a fantastic opportunity to fuse the quantum and physical worlds and deliver a revolutionary INS.”
Xavier Orr, CEO and co-founder, Advanced Navigation
Quantum sensor technology may still be in its infancy, however, the research and development carried out by Advanced Navigation demonstrates that it can be put into practical use. Using a fusion of the Advanced Navigation Boreas digital fibre-optic gyroscope (DFOG) as the classical sensor with quantum sensor hardware, the first inertial navigation systems of this type are being prepared for use in NASA Moon to Mars missions. As the technology is refined and put into more widespread use, the SWaP-C (size, weight, power consumption and cost) will shrink accordingly. The space-qualified system, aforementioned, is approximately the size of a standard refrigerator – this is significantly smaller than many laboratory prototypes and, in time, is expected to reduce to less than one quarter its current size.
For inertial sensing of a moving vehicle, a correctly and carefully fused quantum-classical output derived from appropriate sensors, may become the future for high-grade navigation, both on Earth and off it. Using a classical-quantum system will provide extremely accurate inertial measurement, with virtually no drift, high dynamic range and high bandwidth. The potential for this technology will enable continued precise navigation without requiring recalibration or correction using external references such as satellites, magnetic fields, base station, or stars. This represents an enormous step change in inertial navigation systems that will be revolutionary in applications sensitive to GNSS spoofing/jamming and those that rely on long-term inertial navigation or are entirely divorced from GNSS based navigation.

20 May 2025
Go to Article
30 March 2025
Go to Article